Representando funções por meio de regras e gráficos

Representando funções como regras e gráficos

Vamos começar analisando um exemplo:

Em uma loja, as cenouras custam $ 2,50/lb. O preço que o cliente paga depende de quantos quilos de cenouras ele compra. Outra maneira de dizer isso é dizer que o custo total é uma função das libras compradas. Podemos escrever isso como uma equação.

$$total\: cost=price\: per\: lb\: \cdot \: weight\: bought$$

ou

$$y=2.50\cdot x$$

Uma função é uma equação que mostra a relação entre a entrada x e a saída y e onde há exatamente uma saída para cada entrada. Outra palavra para entrada é domínio e para saída é o intervalo. Como dissemos anteriormente, o preço que o cliente tem que pagar, y, depende de quantos quilos de cenouras, x, que o cliente compra. O número de libras compradas é chamado de variável independente, pois é isso que estamos mudando, enquanto o preço total é chamado de variável dependente, pois depende de quantas libras realmente compramos.

Variável de entrada = Variável independente = Domínio

Variável de saída = variável dependente = intervalo

As funções geralmente são representadas por uma regra de função onde você expressa a variável dependente, y, em termos da variável independente, x.

$$y=2.50\cdot x$$

Você pode representar sua função transformando-a em um gráfico. A maneira mais fácil de fazer um gráfico é começar fazendo uma tabela contendo as entradas e suas saídas correspondentes. Novamente usamos o exemplo com as cenouras

Entrada, x (lb)	Saída, y ($)
0	0
1	2,50
2	5,00
3	7,50

Um par de um valor de entrada e seu valor de saída correspondente é chamado de par ordenado e pode ser escrito como (a, b). Em um par ordenado, o primeiro número, a entrada a, corresponde ao eixo horizontal e o segundo número, a saída b, corresponde ao eixo vertical.

Podemos assim escrever nossos valores como pares ordenados

(0, 0) - Este par ordenado também é referido como origem
(1, 2,5)
(2, 5)
(3, 7,5)

Esses pares ordenados podem então ser plotados em um gráfico.

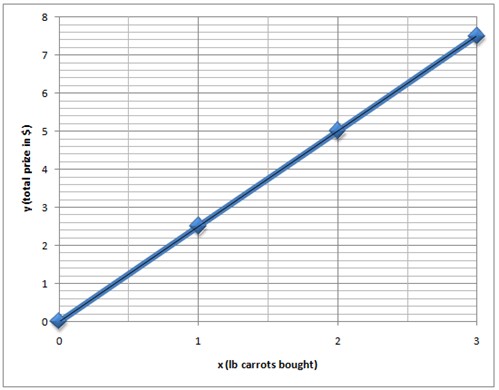
Um pareamento de qualquer conjunto de entradas com suas saídas correspondentes é chamado de relação. Toda função é uma relação, mas nem todas as relações são funções. No exemplo acima, com as cenouras, cada entrada fornece exatamente uma saída que a qualifica como uma função.

Se você não tiver certeza se sua relação é uma função ou não, você pode desenhar uma linha vertical no gráfico. Se a relação não for uma função, o gráfico contém pelo menos dois pontos com a mesma coordenada x, mas com coordenadas y diferentes.

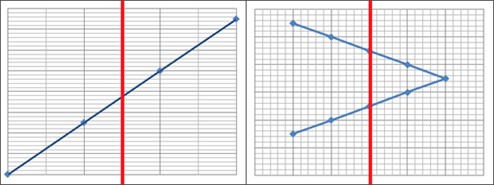
A relação representada no gráfico à esquerda mostra uma função, enquanto a relação no gráfico à direita não é uma função, pois a linha vertical cruza o gráfico em dois pontos.

---

Exercício

Escreva uma regra para a função:

Entrada	0	1	2	4	5
resultado	4	3	2	0	-1